考试公告
干货!浙江事业单位统考6大常考数量关系公式
http://www.zjgwy.org 2024-04-07 来源:永岸公考
数量关系对于大多数同学们来说学习比较难,再加上考试时间不太够用的原因,所以部分同学从一开始对数量的学习就不够重视。
数量关系题目考点众多、灵活多变,永岸公考整理六大公式供各位同学学习,下面先来讲讲等差数列,文章后面附赠其他公式。
一、什么是等差数列
等差数列指的是从第二项起后一项与前一项作差得到一个相同常数的数列。
二、核心概念及公式
1.概念:
项与项数:数列中的每个数字都称为项用小写字母表示,例:a,结合数字所在为位置是数列中的第几个数也就是项数综合表示每一个项。例:首项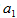 ,第n项:
,第n项: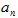 ,中项
,中项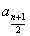
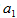 ,第n项:
,第n项: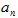 ,中项
,中项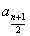
公差:d
前n项和: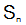
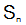
2.公式:
(1)通项公式: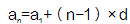 (n为正整数)
(n为正整数)
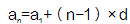 (n为正整数)
(n为正整数) 根据通项公式可知
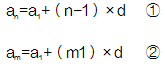
①-②可得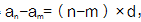 ,由此可知等差数列中的任意两项之差都等于若干个公差,相差的个数就是下角标之差,即等差数列中任意两项只差=下角标只差×公差。
,由此可知等差数列中的任意两项之差都等于若干个公差,相差的个数就是下角标之差,即等差数列中任意两项只差=下角标只差×公差。
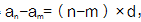 ,由此可知等差数列中的任意两项之差都等于若干个公差,相差的个数就是下角标之差,即等差数列中任意两项只差=下角标只差×公差。
,由此可知等差数列中的任意两项之差都等于若干个公差,相差的个数就是下角标之差,即等差数列中任意两项只差=下角标只差×公差。 (2)求和公式: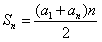
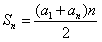
利用中项求和:
当n为奇数时,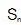 =中间项×项数;
=中间项×项数;
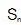 =中间项×项数;
=中间项×项数; 当n为偶数时,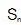 =中间两项和×项数÷2
=中间两项和×项数÷2
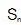 =中间两项和×项数÷2
=中间两项和×项数÷2 三、如何应用等差数列
请记住老师的等差应用秘诀:
核心公式要牢记,提炼概念套公式,
通项就差多个d,角标之差数差距,
偶项求和套公式,奇项中项有关系。
同学们一起用起来!
例1.某剧院有33排座位,后一排比前一排多3个座位,最后一排有135个座位。这个剧院一共有( )个座位。
A.2784 B.2871 C.2820 D.2697
【思路点拨】直接套用基本公式:根据题意,该剧院从前往后每一排的座位数构成公差为3的等差数列,则可以根据第33排求第1排座位有135-(33-1)×3=39个座位,座位总数可以直接利用和公式求解33×(39+135)÷2=2871个。
灵活应用公式:由于座位排数为奇数也就是数列的项数为奇数项,所以座位总数也可以用第17项×项数33求解33项的和,根据第33项可求第17项135-(33-17)×3=87,则座位总数87×33=2871个。
例2.一张考试卷共有10道题,后面的每一道题的分值都比其前面一道题多2分。如果这张考卷的满分为100分,那么第八道题的分值应为多少?
A.9 B.14 C.15 D.16
【思路点拨】10道题目,根据每道题目的分值都比其前面一道题多2分可知10个题目的分值为公差为2的等差数列,十项的和为100。设第1题的分值为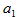 ,第n题的分值为
,第n题的分值为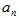 ,则第10题的分值为
,则第10题的分值为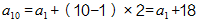 ,利用等差数列求和公式可得100=
,利用等差数列求和公式可得100=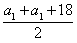 ×10,解得
×10,解得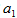 =1,则
=1,则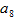 =1+(8-1)×2=15。
=1+(8-1)×2=15。
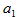 ,第n题的分值为
,第n题的分值为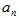 ,则第10题的分值为
,则第10题的分值为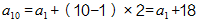 ,利用等差数列求和公式可得100=
,利用等差数列求和公式可得100=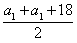 ×10,解得
×10,解得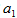 =1,则
=1,则 怎么样?学会了吗?像这样的公式还有很多,同学们不仅仅是简单的背公式,更重要的是要应用的考试中,应试拿分才是学习的目的,下方是整理的数量关系6大公式,赶快收藏学习!
六大公式:
1.等差数列:
(1)通项公式: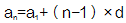 (n为正整数)
(n为正整数)
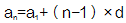 (n为正整数)
(n为正整数) (2)求和公式: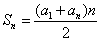
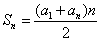
2.利润公式:利润=售价-进价
利润率=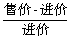 ×100%
×100%
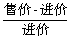 ×100%
×100% 打n折:n= ×10
×10
 ×10
×10 3.行程问题:路程=速度×时间
4.工程问题:工程问题=工作效率×工作时间
5.容斥问题:
两者容斥
I=A+B-A∩B+非A非B
三者容斥
I=A+B+C-A∩B-B∩C-A∩C+A∩B∩C+非A非B非C
6.勾股定理: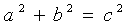
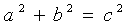

免费学习资源(关注可获取最新开课信息)









