每年国考省考都有同学反映图形推理题考的对称性实在越来越隐蔽了，考完对答案才发现考查的竟然是对称性。

　　在历年真题中，大部分的关于对称性的题目都是比较容易的，且图形的特征也是非常明显，但是依然会有小部分的题目采取的是比较新颖的考法。本文，浙江公务员考试网（www.zjgwy.org）就带大家我们来了解一些关于对称性的不寻常考法。

　　巧解对称性图形

　　先来复习下关于对称性图形的定义：

　　中心对称图形：

　　在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心。

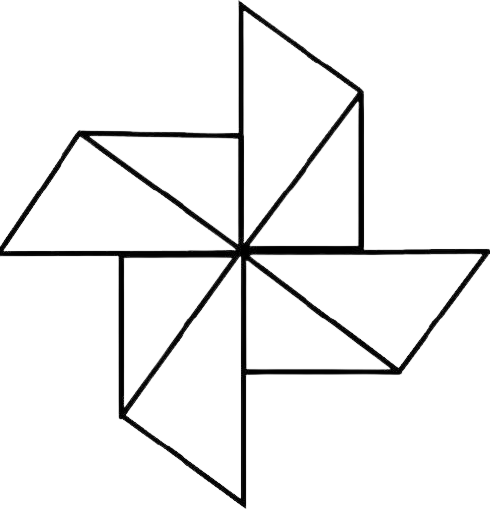
　　轴对称图形：

　　是指在平面内沿一条直线折叠，直线两旁的部分能够完全重合的图形，这条直线就叫做对称轴。

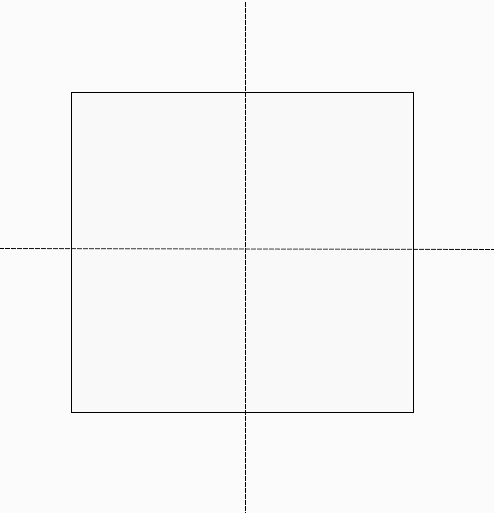
　　我们来通过三道例题来了解下对称性图形的特殊考法：

　　【点拨】

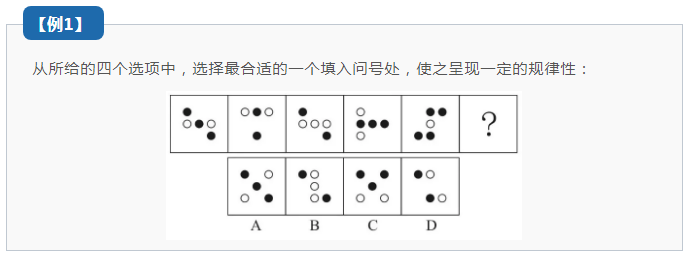
　　看到题干所给的五幅图出现了黑色小圆和白色小圆，不少小伙伴们是不是先考虑到了运算，以及数元素的数量，通过运算以及数元素的数量，就能够发现并没有什么规律。

　　那我们接下来可以考虑将图形看作一个整体。

　　观察题干所给的5个图形发现，出现了一些比较典型的轴对称图形，考虑对称性，题干中的图1至图5分别为：中心对称图形、轴对称图形、中心对称图形、轴对称图形、中心对称图形。

　　即中心对称图形和轴对称图形要交替出现。要符合发现的这个规律，那么我们要选择一个轴对称图形，排除BD两项。因为AC两项都是轴对称图形，所以我们要观察题干中的轴对称图形具有的共同特征有什么，题干中的图2和图4都只有一条对称轴，所以我们要选择只有一条对称轴的轴对称图形，而A项拥有两条对称轴，排除，故答案选C。

　　通过例1，我们了解到了对称性是如何结合黑白点来进行考查的，小伙伴们下次遇到黑白点的题目，且通过常规的思维无法破题时，就可以考虑将题干给出的图形看作一个整体来考查对称性。

　　让我们再来看一道例题，看看黑白点结合对称性还能怎样来出题。

　　【点拨】

　　看到这道题，不少小伙伴的第一选择是不是考虑看移动、旋转等规律。

　　看完题干所给的五幅图，可以发现，并没有这些规律。根据上一道例题给出的经验，我们先考虑将小黑圆看作一个整体，可以发现图3为轴对称图形，图4为中心对称图形，并无其他规律。

　　再考虑将小白圆看作一个整体，可以发现，图1、图3、图5中的小白圆组成的整体为轴对称图形，图2、图4中的小白圆组成的整体为中心对称图形，呈轴对称图形、中心对称图形交替出现的规律。要使被选图形符合此规律，那么被选图形中的小白圆组成的整体应为中心对称图形。

　　观察四个选项，A项中的小白圆组成的整体为中心对称图形，符合规律；B项中的小白圆组成的整体为轴对称图形，排除；CD项中的小白圆组成的整体既不是中心对称图形也不是轴对称图形，排除，故答案选A。

　　通过例2，我们发现出题人是将黑白点中的白点组成的图形来结合对称性来考查，不同于例1考查得“直白”，在解这道题时，有些小伙伴在考虑黑点组成的图形没有发现规律后便直接会选择放弃。

　　下次遇到黑白点的图形，可不要看完黑点组成的图形，就不管白点组成的图形了哦。

　　看完了黑白点是如何结合对称性来考查的，再来看下例3如何利用对称轴进行考查。

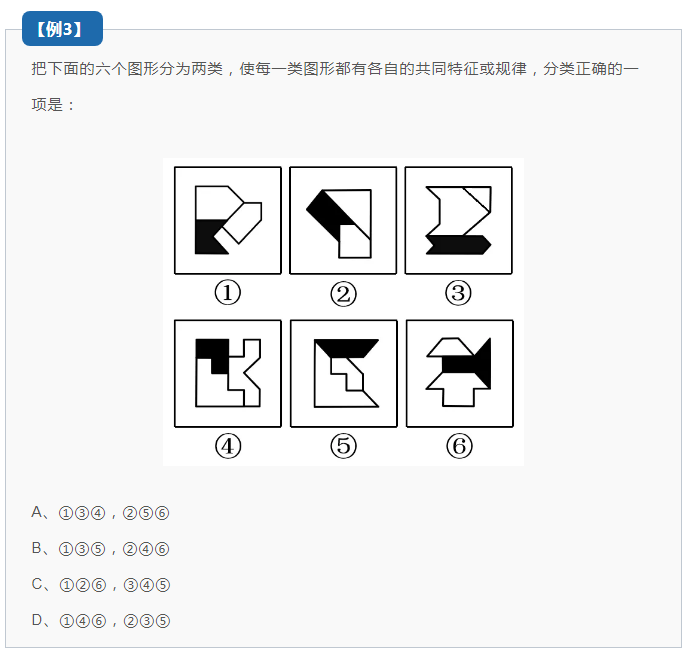
　　【点拨】

　　观察题干给出的六个图形，都由三个图形组成，且两个为白色的图形，一个为黑色的图形。首先考虑将图形都看作一个整体，但是并没有发现存在什么规律。

　　而考虑单看图形中的小图形，可以发现组成图形的三个小图形都是轴对称图形，这个时候我们就可以考虑对称性。将每幅图中的三个图形中的对称轴画出来，如下图所示，红线为黑色图形的对称轴，蓝线为白色图形的对称轴。

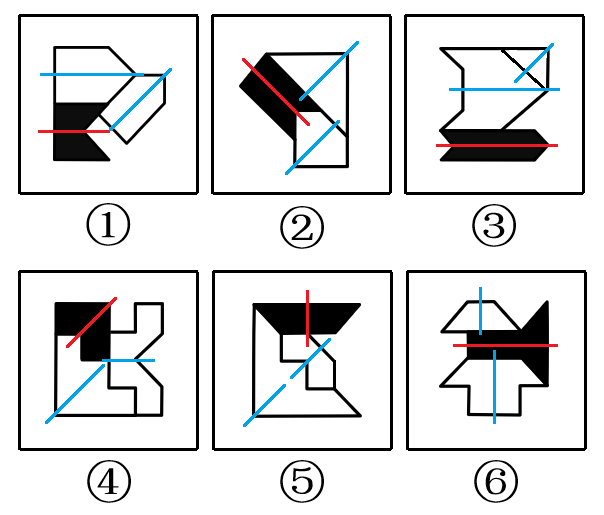
　　图①中的红线与其中一根蓝线平行，与另一根蓝线相交；图②中的红线与两条蓝线均相交；图③④中的红线与其中一根蓝线平行，与另一根蓝线相交；图⑤⑥中的红线与两条蓝线均相交，故以此为两组图形的分类标准，将图①③④分为一组，②⑤⑥分为一组，故答案选A。

　　通过例3，我们可以发现这道题的规律并不是非常冷门、怪异，但对于解这道题而言，小伙伴看到图形，是否能够通过识别图形特征并联想到对称轴的考法是关键。

　　通过上面三道例题，我们了解了一些出题人关于对称性的特殊考法，但通过剖析这三道题，我们还是能够发现，所谓这些特殊的题目都是建立在常规考法的基础上，基于对一些对称图形的特征进行出题的。

　　因此我们需要在日常刷题中多加积累，形成对图形的敏感度，以及在一时难以破题的时候，试着转变思维，或许就能“柳暗花明”。