7月29日更新的2021年浙江公务员考试每日一练是数量关系题，多做公务员考试模拟题练习不仅有利于掌握考点，而且能够帮助保持题感，潜移默化中熟悉命题规律，提高公务员考试做题准确率。

　　1、某款服装降价促销后，每天销量翻倍，获得的总利润增加50%，问每套服装降价的金额为：

　　A、销售的1/4

　　B、销售价的1/8

　　C、利润额的1/2

　　D、利润的1/4

　　2、甲、乙、丙、丁四个工厂共有100名高级技工。其中甲乙两个工厂的高级技工数量比为12:25，丙工厂的高级技工人数比丁工厂少4人，问丁工厂的高级技工人数比甲工厂：

　　A、多6人

　　B、少6人

　　C、多9人

　　D、少9人

　　3、某公司有38名男员工，27名女员工。现要参加集团组织的羽毛球比赛，如采取自由报名的形式，至少有多少名员工报名才能保证一定能从报名者中选出男女选手各8名参赛？

　　A、65

　　B、46

　　C、35

　　D、16

　　4、王大妈在市场承包了一个摊位卖水果，一天收摊后清点钱数时，王大妈发现手上有100元、50元和10元的钞票共48张，合计1760元，其中50元比10元多两张，问100元有多少张？

　　A、8

　　B、6

　　C、4

　　D、2

　　5、将白 、蓝、红三种颜色的背包装到纸箱里，每个纸箱里放5个背包，颜色任意，质监部门需要对产品进行拆箱检查，问至少选多少个纸箱，才能保证一定有两个纸箱里三种颜色的背包数量都一致？

　　A、20

　　B、19

　　C、22

　　D、21

 

　　【下面是参考答案与解析。如果你认为题目或解析有误，可点这里给我们纠错。】

　　1、D

　　第一步：分析问题

　　本题为经济利润问题，未给出具体数值，故可采用赋值法。由于总利润=单件利润×销量，题干给出后来总利润与原总利润的关系，故可根据总利润之间的关系及销量间的关系，找出单件利润之间的关系，求出找出每套服装降价的金额。

　　第二步：计算过程

　　由于每天销量翻倍，故可将原来每天的销量赋值为1，则降价促销后每天的销量为2；

　　由于获得的总利润增长50%，故将原来每天的总利润赋值为2，则降价促销后每天的总利润为2×（1+50%）=3。

　　则原来的单件利润为：2/1=2，降价促销后的单件利润为：3/2=1.5。由于每套服装成本不变，单件利润减少了：2-1.5=0.5，即降价的金额为0.5。由于原单件利润为2，0.5/2=1/4，可知每套服装降价的金额为利润的1/4。

　　第三步：再次标注答案

　　故正确答案为D。

　　2、D

　　第一步：分析问题

　　题干中给出甲、乙两工厂人数的比例关系，故可得出甲、乙两厂人数之和满足的倍数关系，结合丙与丁两厂的人数及四个工厂的总人数，根据奇偶特性，找出甲、乙两厂的总人数，进而求出各厂的人数即可。

　　第二步：计算过程

　　根据“甲乙两个工厂的高级技工数量比为12:25”，可知甲厂人数为12的倍数，乙厂人数为25的倍数，甲乙两工厂人数为12+25=37的倍数；由于四个工厂共100人，故100以内又是37的倍数的只有37、74。

　　根据“丙工厂的高级技工人数比丁工厂少4人”，可知：丁-丙=4，二者之差为偶数，故丁与丙之和也为偶数，由于四厂总人数为100是偶数，因此甲、乙两厂的总人数也为偶数，故甲、乙两厂人数之和只能为74，进而可得甲厂的人数为24人、乙厂的人数为50人。丁、丙两厂之和为：100-74=26。

　　结合：丁-丙=4，丁+丙=26，解得丁=15，丙=11。

　　由于24-15=9，可知丁工厂的高级技工人数比甲工厂少9人。

　　第三步：再次标注答案

　　故正确答案为D。

　　3、B

　　第一步：分析问题

　　本题中出现“至少……保证……”，故为最值问题中的最不利构造问题，解题思路为：最不利+1。

　　第二步：计算过程

　　要保证一定能从报名者中选出男女选手各8名参赛，则最不利的情况为某一性别的人数全部都报名了，另一性别只选出来的7人。由于男员工38人>女员工27人，故最不利的情况即为男员工的全部都报名，而女员工只报名了7人。因此要保证一定能从报名者中选出男女选手各8名参赛，至少有38+7+1=46名员工报名。

　　第三步：再次标注答案

　　故正确答案为B。

　　4、C

　　第一步：分析问题

　　本题给出各面额的总张数及合计钱数，且给出50元比10元面额多两张，故可将10元面额的钞票设为x张，则50元面额的钞票为x+2张，将100元面额的钞票设为y张，再根据总张数及合计钱数列方程、解方程即可。

　　第二步：计算过程

　　根据“100元、50元和10元的钞票共48张”，可知：y+(x+2)+x=48，化简得：y+2x=46，记为①；

　　由于合计1760元，可知：100y+50(x+2)+10x=1760，化简得：5y+3x=83，记为②；

　　联立两个方程，解得：x=21，y=4。即100元的钞票有4张。

　　第三步：再次标注答案

　　故正确答案为C。

　　5、C

　　第一步：分析问题

　　本题中出现“至少……保证……”，故为最值问题中的最不利构造问题，解题思路为：最不利+1。要保证一定有两个纸箱里三种颜色的背包数量都一致，先找出每个纸箱中各色背包的个数情况，把最不利的情况全部找出来，再加1，就能够满足题干的要求。

　　第二步：计算过程

　　因为每个纸箱里有5个背包，则每个纸箱里各色背包的个数有如下分类：

　　有一种颜色的5个，其它两种颜色的各0个，有3种情况；

　　有一种颜色的4个，其它两种颜色分别为0个和1个，有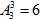种情况；

　　有一种颜色的3个，其它两种颜色分别为0个和2个，有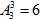种情况；

　　有一种颜色的3个，其它两种颜色各为1个，有3种情况；

　　有一种颜色的2个，其它两种颜色分别为1个和2个，有3种情况；

　　综上，共有3+6+6+3+3=21种可能情况，根据最不利原则，至少要选21+1=22个纸箱，才能保证一定两个纸箱里三种颜色的背包数量都一致。

　　第三步：再次标注答案

　　故正确答案为C。