1.在自然数1至50中，将所有不能被3除尽的数相加，所得的和是：

　　A.865     B.866     C.867     D.868

　　2.有面积为1平方米、4平方米、9平方米、16平方米的正方形地毯各10块，现有面积为25平方米的正方形房间需用以上地毯来铺设，要求地毯互不重叠而且刚好铺满。问最少需几块地毯？

　　A.6块     B.8块     C.10块     D.12块

　　3.有颜色不同的四盏灯，每次使用一盏、两盏、三盏或四盏，并按一定的次序挂在灯杆上表示信号，问共可表示多少种不同的信号？

　　A.24种     B.48种     C.64种     D.72种

　　4.如图所示，在3×3方格内填入恰当的数后，可使每行、每列以及两条对角线上的三个数的和都相等。问方格表内“x”的值是多少？

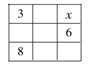
　　A.2     B.9     C.14     D.27

　　5.甲、乙两人沿直线从A地步行至B地，丙从B地步行至A地。已知甲、乙、丙三人同时出发，甲和丙相遇后5分钟，乙与丙相遇。如果甲、乙、丙三人的速度分别为85米/分钟、75米/分钟、65米/分钟。A、B两地距离为多少米？

　　A.8000米     B.8500米     C.10000米     D.10500米

 　 浙江公务员考试网<http://www.zjgwy.org/> 解析 题目或解析有误，我要纠错。

　　1.【答案】Ｃ。解析：能被3整除的数为等差数列3、6、9、……、48，和为（3＋48）×16÷2＝408，1至50的和为（1＋50）×50÷2＝1275，故所求为1275－408＝867。

　　2.【答案】Ｂ。解析：最少情况为一块9平方米，三块4平方米，四块1平方米，选Ｂ。

　　【考点点拨】操作性问题，一般以最小选项考虑。但是本题的切入点在不能选取16平方米的正方形地毯。要让块数最小则每块的面积尽量大，但是从实际操作可知选取16平方米地毯时其余的部分都要用1平方米的来铺，用量不是最小。考虑优先选取9平方米地毯的情况，得到Ｂ项的结果。

　　3. 【答案】C

　　4.【答案】Ａ。解析：设正中间的值为a，有a＋6＝8＋3，可得a＝5。由3＋a＝x＋6，可得x＝2。

　　5.【答案】Ｄ。解析：甲、丙相遇时，甲比乙多走了的距离为乙、丙相距的（75＋65）×5＝700米，所以此时三人都已步行了700÷（85－75）＝70分钟，故Ａ、Ｂ两地距离为（85＋65）×70＝10500米。